Après avoir résolu le problème de positionner une information sur une surface sphérique grâce au système de coordonnées géographiques, le second problème auquel sont confrontés les cartographes, est celui de déplier le globe, pour le mettre à plat sur une feuille (ou sur un écran d’ordinateur).
Un sphéroïde ne peut pas être aplati sur un plan, à l’instar d’une peau d‘orange, qui va se déchirer. La représentation de la surface de la terre en deux dimensions provoque une distorsion de la forme, de la surface, de la distance et de la direction des données.
La projection cartographique est un ensemble de techniques géodésiques permettant de représenter une surface non plane (surface de la Terre, d’un autre corps céleste, …) dans son ensemble ou en partie sur la surface plane d’une carte. En clair, on sait que la Terre n’est pas plate, et la projection cartographique sert donc à aplanir une partie de la surface terrestre. Digérentes projections provoquent digérents types de distorsions. Certaines projections sont conçues pour minimiser la distorsion d’une ou deux caractéristiques des données. Une projection peut ainsi conserver la surface d’une entité mais en modifier sa forme.
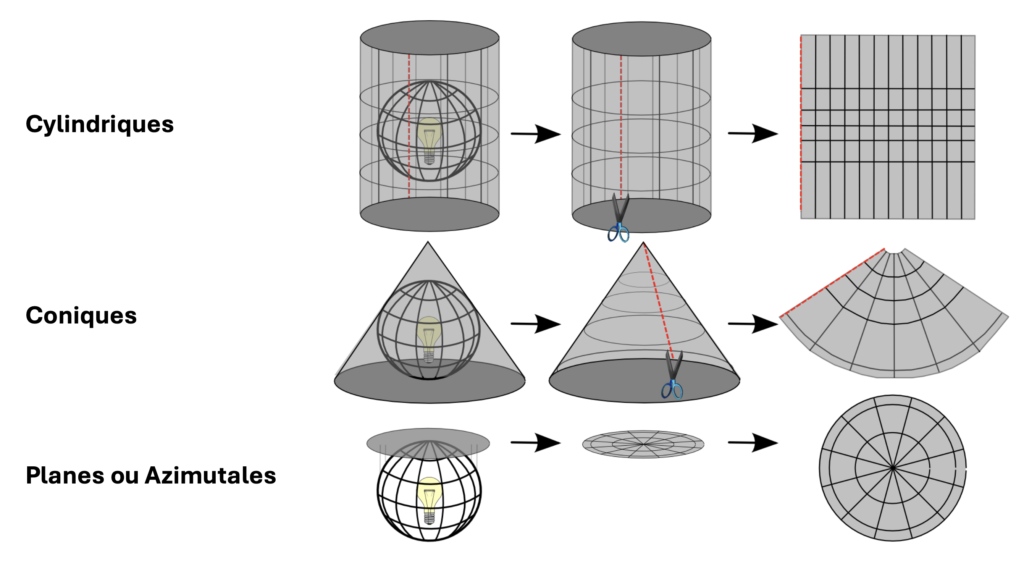
Les cartes étant plates, certaines des projections les plus simples sont faites sur des formes géométriques qui peuvent être aplaties sans étirement de la surface. Elles sont appelées surfaces développables. Les exemples les plus courants sont les cônes, les cylindres et les plans. Une projection cartographique projette systématiquement des emplacements de la surface d’un sphéroïde vers des positions représentatives sur une surface plane à l’aide d’algorithmes mathématiques. Après projection, les coordonnées planes ainsi obtenues permettent des mesures directes sur la carte (angles, surfaces) mais toutes représentations planes engendrent des déformations (les distances ne sont jamais conservées).
Il existe de nombreux systèmes de projections. On peut les regrouper en trois catégories :
Exercice 2
Testez l’effet de différents projections cartographiques sur notre représentation du monde.
- Rendez-vous sur https://www.sciencespo.fr/cartographie/graticule/
- Cliquer sur
Créer votre propre fond de carte - Sur la page suivante, laisser la carte à l’échelle du monde et cliquer sur Continuer
- Cliquer sur Indicateur de Tissot en bas à gauche pour mieux visualiser l’effet des déformations pour chacune des projections que vous allez réaliser.
- Dans le menu déroulant Projections, tester les différentes projections proposées.
- Pour chacune d’entre elle, prenez le temps de cliquer sur En savoir plus pour comprendre la raison qui a poussé les cartographes à créer cette projection.
Le système de projection auquel nous sommes le plus souvent exposé s’appelle le WGS84 / Pseudo-Mercator. Cette projection est utilisée pour les cartes marines car elle conserve la forme des continents et permet la conservation des angles, pratique pour la navigation avec un compas. La projection de Mercator est ainsi connue pour ses méridiens et ses parallèles qui se coupent à angle droit. Mais elle modifie les distances et les surfaces, surtout sur l’axe Est-Ouest. Ce système a été largement popularisé par l’application Google Maps et est devenu le standard pour la cartographie web. Son numéro d’identifiant unique est le EPSG:3857.
Le système de projection officiel utilisé en France s’appelle le Lambert 93. Cette projection permet une représentation extrêmement précise des données sur l’ensemble de la France métropolitaine contriarement au Pseudo-mercator (précision de 2m). Il s’appuie sur la même ellipsoïde que le WGS84 et est donc compatible avec tous les relevés GPS. C’est ce système qui sera utilisé dans les données que nous téléchargerons sur les sites des institutions françaises. Cette fois, les données ne sont plus positionnées en degrés, mais sont projetés dans un plan avec des coordonnées x et y qui sont spécifiques à chaque projection.
